Introduction

I’m not exactly sure what it is about programming languages that I find so interesting, but for some reason I just can’t seem to shake the fascination I have for them. Perhaps it is the relatively simple algorithms and techniques that are used to perform what appears to the casual observer to be ‘black magic.’ How do they get input code, which can be constructed in any number of different ways, at virtually any length, to do what the user (programmer) wants? I’ll show you how I built my own interpreter using Gold Parser Builder, and Arsène von Wyss’s brand new BSN-Engine.

Background

All interpreters generally follow the same basic steps. Essentially some input stream is translated into a hierarchical tree of nodes representing the different operations it is to perform. After this hierarchical structure, known as an Abstract Syntax Tree (AST) is constructed, each node is evaluated from the bottom up until the root is reached and the ‘program’ completes. These nodes can either serve as expressions which return values to their parent callers, or statements which simply act to produce ‘side effects’ — changes in the execution environment. (Examples of side effects would be setting variable values, or printing text to the output buffer.)

The first step in the process I just described is called translation. The input stream is passed over by a unit known as a ‘scanner.’ As a piece of input matches a known pattern, it is ‘recognized’ as a chunk called a token. (If a pattern of input fails to match any of the defined tokens in the language, then this condition is a type of syntax error known as a token error.) The order and arrangement of tokens is then compared against a series of expected token configuration patterns known as ‘rules’ until a ‘match’ is found. If no match for a given series of tokens is found in the rules of the language, it is another kind of syntax error, known as a ‘rule error.’ Rule errors are probably the most commonly encountered type of syntax error. It literally means that there is no rule in the defined language syntax (often described by a grammar which we will get to in a bit,) which would recognize the present arrangement of tokens.

At first glance, Devin Cook’s Gold Parser Builder (GPB) seems to promise an easy solution. It’s a complete language grammar development environment. You can design and test a full language grammar right in the IDE. And there is even this handy little feature that allows you to generate skeleton code… To anyone like me who has stumbled upon this toolkit, it almost seems too good to be true. And in some ways, it is! For all but a few cases, the code skeletons that GPB generates are a long way away from anything that can actually be called an interpreter or a compiler. Still left to the user is the monumental task of translating the tokens and rule reductions provided by the GOLD engines and their respective code templates into an AST and then into an executable form. You CAN do it the hard way, and implement every non-terminal rule as a node for your AST, and wire them up ‘by hand’ as has been demonstrated by countless examples all over the web. (There are even a few of them here on CodeProject!) But, if you’re just out to learn how this works, or to say that you’ve done it, it’s so much work that you could become rather understandably discouraged. Perhaps you'd even throw in the towel with an exclamation like “Ok, enough of this, I get it. I just don’t want to DO it.” (Yes, that’s a slightly autobiographical reference to my own first experiences, circa 2006.) But if this has happened to you, or you’re just looking at all of this and starting to get nervous already, just wait a second! There is now a new way!

Typically, I avoid subscribing to mailing lists and even shy away from using my ‘real’ email address on public forums. But GOLD Parser has been something which I have believed in ever since I first discovered it, and I do catch the occasional email crossing the list. Recently, one particular announcement caught my attention, from a certain Arsène announcing the arrival of the new BSN engine on the scene.

What’s an Engine?

The way the GOLD Parser system works is that you use the GPB application to create an LALR(1) grammar in something that is a cross between BNF notation and EBNF notation. It’s actually quite readable (for humans too,) even compared to the similarly purposed YACC/Bison tools. The grammar, after being validated and tested in the GPB IDE can be used to export a binary representation of the DFA and LALR Parse Tables used to recognize the defined language. This Compiled Grammar Table (CGT) as it is called, is then used by any number of ‘engines’ or support systems to implement the generated parser in a variety of different host platforms. For example, there are engines for C++, Java, the D language, and of course, .NET. Typically they all consume the CGT and produce a stack or stream of productions (orderly arrangements of tokens,) which must then be handled by code produced by the language (or other parser-based tool) implementers. Now, granted, a lot of heavy lifting is already handled at this point by the builder and the engines, but there is still a lot left to do.

Enter BSN

The BSN engine consumes and analyzes the CGT, and also produces tokens from an input stream, but the user (user in this case referring to the programmer implementing a language with them), never sees tokens and productions directly! All that the user sees are the tokens wrapped into compact objects that represent nothing but the most essential moving parts of the translated AST. The rest is abstracted away by the engine (which itself may better be referred to as a Framework. And in case you’re wondering, I’m not interested in debating the definition of this term in the comments. Thanks.) At this point, I can’t really describe it without an example, so let’s get one of those.

I’ve taken a sample grammar originally designed by Devin Cook to test GOLD engines, added and changed a few things, and implemented it as a Read-Evaluate-Print-Loop (REPL) interpreter. In the form into which I’ve molded it, it’s very much like, well, every other imperative language you’ve ever seen before. Let’s have a look at the grammar first:

Warning: I'm not going to explain everything in detail about the grammar, so if you need to brush up on your GOLD notation, check out the official GOLD website at http://devincook.com.

The Grammar 

"Name"    = 'Simple'
"Author"  = 'Devin Cook (dave dolan added stuff)'
"Version" = '3.0' 
"About"   = 'This is a very simple grammar designed for use in examples'

"Case Sensitive" = False 
"Start Symbol"   = <Statements>

{String Ch 1} = {Printable} - ['']
{String Ch 2} = {Printable} - ["]

Id            = {Letter}{AlphaNumeric}*

! String allows either single or double quotes

StringLiteral = ''   {String Ch 1}* ''
              | '"'  {String Ch 2}* '"'


NumberLiteral = {Digit}+('.'{Digit}+)?


<Statements> ::= <StatementOrBlock> <Statements>
               | <StatementOrBlock> 

<StatementOrBlock> ::= <Statement>
                       | begin <Statements> end 

<Statement>  ::= print <Expression> 
               | print <Expression> read ID  
               | ID '=' <Expression> 
               | loop <Statements> while <Expression> 
               | for '(' <Statement> ';' <Expression> ';' <Statement> ')' do <Statements> end
               | while <Expression> do <Statements> end
               | if <Expression> then <Statements> end
               | if <Expression> then <Statements> else <Statements> end
               | function ID '(' <OptionalParamList> ')' begin <Statements> end
               | return <Expression>              

<OptionalParamList> ::= <ParamList>
                      |

<ParamList> ::= ID ',' <ParamList>
              | ID


<Expression>   ::= <Expression> '>'  <Add Exp> 
                 | <Expression> '<'  <Add Exp> 
                 | <Expression> '<=' <Add Exp> 
                 | <Expression> '>=' <Add Exp>
                 | <Expression> '==' <Add Exp>
                 | <Expression> '<>' <Add Exp>
                 | <Add Exp> 

<Add Exp>      ::= <Add Exp> '+' <Mult Exp>
                 | <Add Exp> '-' <Mult Exp>
                 | <Add Exp> '&' <Mult Exp>
                 | <Mult Exp> 

<Mult Exp>    ::= <Mult Exp> '*' <Negate Exp> 
                | <Mult Exp> '/' <Negate Exp> 
                | <Negate Exp> 

<Negate Exp>  ::= '-' <Value> 
                | <Value> 

<Value>       ::= ID           
                | StringLiteral
                | NumberLiteral                
                | ID '(' <OptionalArgumentList> ')'
                | '(' <Expression> ')'
               
<OptionalArgumentList> ::= <ArgumentList>
                         |

<ArgumentList> ::= <Expression> ',' <ArgumentList>
                 | <Expression>

Yes, that’s it. Just that bit defines the entire language, syntactically. Every program you can ever write in Simple 3 is encoded in that tiny little space. The things on the left of the ‘::=’ are called productions, and the things on the right are known as rules. If the parser matches any of the rules of a production, the stream of tokens and perhaps other productions that it contains are ‘reduced’ to that production. If you would like to execute a production, you have to know all of the ‘meaty’ details within it. For example, looking at the <Statement> rule: “ID = <Expression>.” This rule represents an Assignment Statement production because it is, well, a  ‘statement’ that performs a variable assignment. Statements, in Simple 3, can alter the state of the application, but they cannot return values. What you see in the assignment statement production is the assignment of an expression’s value (which itself can be one of any number of different rules matching the Expression production defined later in the grammar) to an identifier (in this case, a variable.) Expressions on the other hand, they return values and may or may not produce side effects. (Probably shouldn't.)

Now, the code part of this is actually pretty basic. First, I have to build a very few support structures to flesh out what I just said.

A statement can be executed, but returns no value:

    public abstract class Statement : Simple3Token{
        public abstract void Execute(Simple3ExecutionContext ctx);
    }

An expression returns a value:

    public abstract class Expression : Simple3Token{
        public abstract object GetValue(Simple3ExecutionContext ctx);
    }

Since the Statement and Expression classes represent productions, and not specific implementations of the number of rules that can be reduced to them, we use abstract classes with abstract methods that implement the required behaviors.

What’s an Execution Context?

If you already know what one is, you’d think that an execution context is very much what it sounds like. However, if you’re new to this stuff, don't worry, it’s pretty easy to understand. Basically, it’s the environment in which the user code executes. In the ‘real world,’ execution contexts can be very complex beasts loaded with features that help to support optimization and a whole host of other things. For my Simple 3 example, it’s a structure that merely has a hash table to hold all of the variables, a return value stack for function calls, a reference to the parent context, and a reference to each the input and output streams. The main program has a global execution context, and each function call gets its own execution context. All execution contexts share a reference to a single global return value stack, even though they have their own variable storage. When a reference is made to a variable, it’s first checked against the current execution context. If the variable isn’t found, it’s deferred to the parent. If it gets the whole way to the top, and the referenced variable is still not found, a runtime exception is thrown indicating that it’s an undefined variable. (To be clear, the way one defines a variable in this language is by assigning it a value. Defining a variable, in the case of this language, should not be confused with the concept of ‘variable declaration,’ which is found in many other languages. You cannot declare a variable in Simple 3.)

How Do We Get from Rules in a Grammar to Calling methods of These Tiny Little Objects?

In the olden GOLD days, (a reference to the pre-BSN engine world,) one would write a large block of code to consume the list of productions handed down from the GOLD engine and create container objects for each of the terminals and non-terminals. Each of the non-terminal containers is itself a container of still more child objects, which would have to be consumed in the same manner. The child objects are known as Abstract Syntax Nodes. This constructed container of containers and their child containers is the previously mentioned AST. Constructing an AST before you can consume it is the bulk of the work when you use most any of the GOLD engines. To make an interpreter from an AST (which is the path of least resistance to a working language implementation), you add some methods that execute or evaluate each of them with respect to an execution context. This is essentially creating ‘an executable AST.’ This is what I do in the Simple 3 example, and this whole creation of nodes from tokens process still occurs as I have described it, but BSN engine hides most of it from the user (language implementer). With the BSN engine, the tree construction is ‘mapped’ by the user at design time by annotating stripped down versions of only the nodes that ‘do something’ with the bits of the grammar they represent. (Action nodes are commonly referred to as 'semantic actions' in other literature.)

A Closer Look at an AST

An AST isn’t all that complicated. It’s just a node graph representing the ‘program.’

In an AST, the operation or semantic action is the node (non-terminal node), and the operands are the children. Operands can consist of other non-terminal nodes, or terminal nodes which are concrete elements of syntax that represent values, punctuation, or keywords. The deepest children (leaf nodes) are evaluated and pass their values up as operands to the parent operation until the top operation is finally carried out.

Let’s start small and look at one for the expression 1 + 2 * 3.

Simple AST

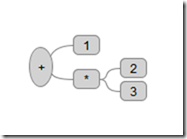
AST Expression Image 1 + 2 * 3

When this expression is evaluated, the deepest non-terminal is '*' with leaves '2' and '3'. That would of course be 2 * 3 or when evaluated, 6. Passed up a level to the '+' operator as the second operand, the entire tree at that point becomes:

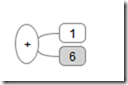
AST Expression Image 1 + 6

Of course this is now 1 + 6, and easy enough to see it will evaluate as 7.

The operations represented by the non-terminals can be quite a bit more complex than simple arithmetic operators, but this is the idea behind how an AST lives and breathes.

The BSN engine makes it really simple to generate an AST, once you’ve used GPB to generate a CGT from your grammar.

Starting Simple

Virtually every example of how to make a compiler or interpreter I have ever seen uses simple arithmetic expressions, and stops there. It’s not hard to imagine why, I mean, wiring up nodes from the stack of reduced productions is a real pain. But I decided that I’m not going to be that guy, and instead go for the entire language here.

I know that all binary operations will have two operands, a left and a right. That’s really all I can say that all binary operations have in common, so I create an abstract class, BinaryOperator that has that single abstract method. It’s also possible that I may not want the evaluation process to try and seek type agreement because I know a particular kind of operator always has a predictable kind of operand. For this, I’ll have a flag that allows for it to skip the type checker.

    public abstract class BinaryOperator : Simple3Token{
        public virtual bool SkipConversion{
            get { return false; }
        }
 
        public abstract object Evaluate(object left, object right);
    }

Concrete instances of these operators are mapped to syntactic terminals (meaning they cannot be reduced to deeper constructs containing other constructs) by adorning the class with a Terminal attribute. For example, the “+” operator looks like this:

    [Terminal("+")]
    public class PlusOperator : BinaryOperator{
        public override bool SkipConversion{
            get { return true; }
        }
 
        public override object Evaluate(object left, object right){
            return Convert.ToDouble(left) + Convert.ToDouble(right);
        }
    }

The attribute is a ‘handle’ for the BSN engine to grab on to when it is constructing the node building classes for this particular grammar. Basically it means, “when you see a ‘+’ terminal, create an instance of this class and stuff it into the AST.”

This gives us a little taste of how nice the BSN engine makes the process of constructing an AST. We just declare that this class will be instantiated when you get this terminal. Done. The rest is abstracted away by the engine doing its work.

Now that’s pretty neat, but the real bit that feels like black magic is when we go to the non-terminals. Instead of adorning the class itself, a non-terminal node adorns the constructor with the actual text representation of the grammar rule that cases it to be called. As is clearly shown below, you can string up a bunch of them for a number of possible variations.

BinaryOperation Class

 public class BinaryOperation : Expression{
        private readonly Expression _left;
        private readonly BinaryOperator _op;
        private readonly Expression _right;


        [Rule(@"<Expression> ::= <Expression> '>' <Add Exp>")]
        [Rule(@"<Expression> ::= <Expression> '<' <Add Exp>")]
        [Rule(@"<Expression> ::= <Expression> '<=' <Add Exp>")]
        [Rule(@"<Expression> ::= <Expression> '>=' <Add Exp>")]
        [Rule(@"<Expression> ::= <Expression> '==' <Add Exp>")]
        [Rule(@"<Expression> ::= <Expression> '<>' <Add Exp>")]
        [Rule(@"<Add Exp> ::= <Add Exp> '+' <Mult Exp>")]
        [Rule(@"<Add Exp> ::= <Add Exp> '-' <Mult Exp>")]
        [Rule(@"<Add Exp> ::= <Add Exp> '&' <Mult Exp>")]
        [Rule(@"<Mult Exp> ::= <Mult Exp> '*' <Negate Exp>")]
        [Rule(@"<Mult Exp> ::= <Mult Exp> '/' <Negate Exp>")]
        public BinaryOperation(Expression left, BinaryOperator op, Expression right){
            _left = left;
            _op = op;
            _right = right;
        }

        public override object GetValue(Simple3ExecutionContext ctx){
            object lStart = _left.GetValue(ctx);
            object rStart = _right.GetValue(ctx);

            object lFinal;
            object rFinal;

            if (!_op.SkipConversion){
                TypeChecker.GreatestCommonType gct = TypeChecker.GCT(lStart, rStart);

                switch (gct){
                    case TypeChecker.GreatestCommonType.StringType:
                        lFinal = Convert.ToString(lStart);
                        rFinal = Convert.ToString(rStart);
                        break;
                    case TypeChecker.GreatestCommonType.BooleanType:
                        lFinal = Convert.ToBoolean(lStart);
                        rFinal = Convert.ToBoolean(rStart);
                        break;
                    case TypeChecker.GreatestCommonType.NumericType:
                        lFinal = Convert.ToDouble(lStart);
                        rFinal = Convert.ToDouble(rStart);

                        break;
                    default:
                        throw new TypeMismatchException( );
                }
            }
            else{
                // let's not put square pegs in round holes. 
                // Sometimes the operators can 'universally convert'
                // like the '&' operator will always convert to a string. Always.
                lFinal = lStart;
                rFinal = rStart;
            }
            return _op.Evaluate(lFinal, rFinal);
        }
    }

The engine will figure out what kind of expression to fill in for the ‘left’ and ‘right’ parameters by matching them to the classes adorned with the appropriate rules. This is done recursively until the entire tree is constructed. ALL we have to do is specify the rules that match the classes on the right constructors and implement the bare minimum number of non-terminal nodes.

Which Non-terminals Need to be Implemented as Classes?

Some non-terminal productions contain rules purely composed of other non-terminals, and thus do not need a concrete class. These have been given a name: transient non-terminals. They exist to resolve conflicts, or glue together combinations of non-terminals in formation. These transient non-terminals do not represent any particular executable code, so we don’t have to do anything with them in our source code. In GOLD engine parlance, a stack of reduced productions which elides the transient non-terminals is known as one that has been trimmed. If you look at the grammar tester tool in GPB, you can see that there is an option to Trim Reductions. You can see it in action by checking this box, and the final stack of productions will contain no transient tokens.

Of course, there is no box that one needs to check in the case of implementing the nodes using the BSN engine. Just ‘forget’ to implement them, and they’re treated as transients (or an error, if they really aren’t transient, which we will see later.)

How Do We Know If We’re Done, For Sure?

One of the quintessential features of the BSN engine is that when it is initialized and loads a grammar, it fully analyzes the structure of all of the nodes, and will spit out a report of any errors it finds. To demonstrate, I’ll comment out the PlusOperator’s Terminal attribute and try to run the code again.

The semantic engine found errors: Semantic token is missing for terminal '+'

The factory for the type SimpleREPL.Simple3.BinaryOperation used by rule '+' expects a SimpleREPL.Simple3.BinaryOperator on index 1, but receives a SimpleREPL.Simple3.Simple3Token.

“Wow, oh yeah, I forgot to adorn the PlusOperator class with a Terminal attribute!” Saved me a pile of time! Finding a token that you’ve missed isn’t the only trick that the analysis enables you to do. You can also run it on a brand new CGT file and it will kindly print out a list of all of the classes you’re going to have to implement to make it work. Kind of like a pre-flight checklist, you can just cross them off (or re-run the program to generate a new list,) and you know when it’s time to rock and roll. Here’s the code that I have at the front of the REPL that initializes everything in the right way that I get this list printed to the console if something is wrong:

    // this is lifted directly (almost) from the example code that comes with the engine
    CompiledGrammar grammar = CompiledGrammar.Load(typeof (Simple3Token), "Simple3.cgt");
    var actions = new SemanticTypeActions<Simple3Token>(grammar);
    try{
        actions.Initialize(true);
    }
    catch (InvalidOperationException ex){
        Console.Write(ex.Message);
        Console.ReadKey(true);
        return;
    }

What about ‘Sequence’ non-terminals?

I’m glad you asked about Sequences! Sequences are non-terminal tokens that can optionally include an array of zero to n child tokens. For example:

<Statements> ::= <StatementOrBlock> <Statements>
               | <StatementOrBlock>

Multiple statement tokens in a row, or just a lonely statement token matches the production <Statements>. We might even say that this is a sequence of statements. (Now the name makes sense!)

There is a special pattern construct, which von Wyss illustrates in the wiki section of the BSN project website, known as the Sequence pattern. For Simple 3, all of the sequence (list type tokens) are mapped into constructors of this class.

Sequence Class

public class Sequence<T> : Simple3Token, IEnumerable<T> where T : Simple3Token{
        private readonly T item;
        private readonly Sequence<T> next;


        public Sequence()
            : this(null, null){
        }

        [Rule(@"<ParamList> ::= Id", typeof (Identifier))]
        [Rule(@"<ArgumentList> ::= <Expression>", typeof (Expression))]
        [Rule(@"<Statements> ::= <DelimitedStatement>", typeof (Statement))]
        public Sequence(T item)
            : this(item, null){
        }

        [Rule(@"<ParamList> ::= Id ~',' <ParamList>", typeof (Identifier))]
        [Rule(@"<ArgumentList> ::= <Expression> ~',' <ArgumentList>", typeof (Expression)]
        [Rule(@"<Statements> ::= <DelimitedStatement> <Statements>", typeof (Statement))]
        public Sequence(T item, Sequence<T> next){
            this.item = item;
            this.next = next;
        }

        #region IEnumerable<T> Members

        public IEnumerator<T> GetEnumerator(){
            for (Sequence<T> sequence = this; sequence != null; sequence = sequence.next){
                if (sequence.item != null){
                    yield return sequence.item;
                }
            }
        }

        IEnumerator IEnumerable.GetEnumerator(){
            return GetEnumerator();
        }

        #endregion
    }

You might notice that the Rule attributes have more complicated parameters now.

In this example, since ArgumentLists have a comma separating each comprising expression, we want to skip it. The only parts of the rule that contribute anything to the node we’re building are the first, <Expression>, and the third, <ArgumentList>. The throw-away comma terminal is marked as such by the ~ symbol. All terminals marked with ~ are ignored when mapping the parameters to constructors. Also note, the type of enumerable node is specified as the second parameter to the Rule attribute constructor. Here's a closer look:

[Rule(@"<ArgumentList> ::= <Expression> ~',' <ArgumentList>", typeof (Expression)]

Tell Me Again What the TypeChecker is?

In this case, the type checker looks at multiple parameters, determines their ‘greatest common type’ or the type to which they all can be converted for use in the operation. If you try to add the number 12 to a string “12”, it recognizes that the greatest common type is ‘number’ in this case, since both can be converted to a number. The way that Simple 3 does this isn’t a foolproof plan for use in all languages, but it does the job well enough for the purpose of this interpreter. (Simple 3 supports a very limited set of types, and does not allow the user to create his own.)

So, What Does ‘code’ Look Like in our Example Language?

Here’s some of the quintessential examples that one must use to prove that a language is a language.

Hello world:

    print "hello world"

99 bottles of beer:

    x = 99
    while (x > 0) do
       print x & " bottles of beer on the wall. Take one down and pass it around..."
       x = x - 1
    end

OR

for ( x = 99; x > 0; x = x - 1)  do
   print x & " bottles of beer on the wall. Take one down and pass it around..."
end

If you want to, you can write these things all on one single line. That's cool and all, and sure it's a language we might not really have a need for, but the point is that we have a working interpreter, and she floats! The best way to play around with this is to run the REPL app that comes in the download. (Just load up the project file into Visual Studio 2010 – even Express Edition works OR MonoDevelop 2.4 or higher and debug it, and you’re off.)

The REPL

The REPL interpreter you can download above actually uses a single execution context as a ‘global’ environment. It reads a line of text and aggregates it into a single input line until it encounters two blank lines. When it hits two blank lines, the preceding text is processed (parsed and evaluated) as input code. You can split up anything on to multiple lines, but you cannot leave blank lines between it, or the REPL will start processing before you finish your code snippet and it will throw a syntax error.

The > indicates “start of input” and the “Ok.” acknowledges that what you have just input has been read as a valid piece of code just before it is executed.

Note: You can toggle the timer feature by entering ‘timer’, which will, as the name implies, time things when it is on. In particular, the parse and the execution (each timed separately.)

> timer
 
Timer toggled to ON.
> print "hello world"
 
Parse: Elapsed: 1ms
Ok.
 
hello world
Execution: Elapsed: 1ms
> timer
 
Timer toggled to OFF.
>

Weird Features of the Fake (But Technically Real) Language

You can declare functions, and call them. You can declare functions inside functions. If you name a function something that is already used in a parent scope, you ‘hide’ the parent for that scope. Essentially, this means that the deepest function wins.

 
> function abc(x, y)
  begin
    function abc(g,h)
      begin return g + x + h end
    return x + y + abc(x,y)
  end
 
Ok.
> print abc(1,2)
Ok.
7
>

Pretty crazy huh? I’m not sure why you’d want to do that, but that’s how the language works.

Why (and How?)

Each function call, like any statement or expression, executes in an execution context. When you call a function, in Simple 3, a new context is created that shares the input/output streams with the parent context, shares the return value stack, but has its own set of function definitions and its own set of variables. When it cannot find a referenced function or variable, it passes the reference to the parent context to check there… and so on and so on, up to the top. If it gets to the top without finding it, an exception is thrown. This behavior naturally causes the ‘deepest one wins’ without any special consideration added.

Take a look at the code. Take a look at the engine website. Play around with Gold Parser Builder, and see what you can come up with. This is fun stuff, and believe it or not, understanding how this process works provides you with a lot of basic insight that generally applies to so many areas of computing. You learn how parsers recognize text. You learn how operator precedence is implemented. You visualize what a function call is. After a while, you will find ways to weave this new perspective on how the black box compiler is arranging your code into executable details into your troubleshooting and debugging process with your own code.

My language, as the name implies, and this example implementation of an interpreter are both indeed simple, and they are not optimized either for usability, readability, or speed of execution; however, conceptually all of the parts are there: the recognition of input, translation to an AST, and finally execution of code.

To learn more about how a particular language feature is implemented, I suggest throwing some break points in the node code and looking around while it’s running. It’s probably the best way to fully understand how each feature works. If you want to improve Simple 3 or feel that I should show something a different way, let me know, and I’ll update this article and the code (maybe).

ABOUT THE CODE

There is no real dependency on any particular IDE, but the project files are built using VS 2010. It targets .NET 3.5, (Mono 2.6) and also builds and runs in MonoDevelop version 2.4. (It may work in earlier versions of MonoDevelop, but was tested on a linux-based host with version 2.4.)

Note: The source code for this project has been added to a Google Code repository and will be updated there.

History

  • November 22, 2010: First edition, hot off the presses