快手网

Introduction

Creating a mathematical expression evaluator is one of the most interesting exercises in computer science, whatever the language used. This is the first step towards really understanding what sort of magic is hidden behind compilers and interpreters. A mathematical expression evaluator is an "interpreter". An interpreter is a program that is able to dynamically execute commands written is a defined language. Compilers are different from interpreters in the way that programs are transformed into a processor-specific language -- i.e. assembler -- hence allowing better performance.

Therefore, with a mathematical expression evaluator, you should be able to dynamically calculate formulas like: 2 + 5 * 3. This is very useful if, for instance, you have to parameterize parts of your applications and need to execute some calculations. The language used by this interpreter is the "mathematical language". Concretely, a programmer who would like to use the mathematical expression interpreter would use it as below:

Collapse | Copy Code

Console.WriteLine("Please enter an expression to evaluate: ");
string text = Console.ReadLine();
Expression e = new Expression(text);
Console.WriteLine(e.Evaluate());

The steps of building an interpreter are somehow very simple and all interpreters have the same behavior. Thus, all of the things explained here can be used to create another interpreter for any other language.

Approach

Defining the Language

The first step of building an interpreter is to define the language to interpret. This language will be defined in the BNF (Backus-Naur form) notation, which is itself a language to describe other languages.

Lexer and Parser

Our program must be able to read and understand all of the phrases that will be given to it. To read those phrases, we will create a "lexer". To understand them, we will need what is called a "parser". A lot of programmers still use the ugly hand-made "switch case" pattern to detect elements in an expression. This makes the grammar not maintainable and not very powerful by disallowing pre-compilation. In this article, the lexer and the parser will be generated by an external dedicated tool. The most-known ones are Lex and Yacc, but we will focus on ANTLR for its ease of use and its ability to generate C# code.

Execution Engine

As the parser and the lexer are created, the interpreter can start executing the hidden meaning behind the phrases.

Stories

Principle

All the functionalities we want in our Framework need to be defined before the language itself.

The User Should Be Able to Evaluate the String Representation of a Logical Expression

A logical expression can be a calculus expression or any other expression returning a value. The Framework should be able to take a string representing an expression as an entry and give back the calculated result of this expression. For instance, the evaluation of the string 2 + 2 should return the integer value 4.

The User Should Be Able to Define Parameters

Parameters are useful for executing the same expression multiple times by varying some parts of it. For example, to calculate the square of a number we could parameter this number: [number] * [number]

The User Should Be Able to Use Predefined Mathematical Functions

In any logical expression, mathematical functions are used whether they be operators like +, -, *, / or even pow(), cos() and so on and so forth.

The User Should Be Able to Use His Own Functions

This might be the most useful functionality, as we can't predict all the scenarios of the use of the Framework. A new business or application-specific function could be needed in an expression. Thus, the user should be able to use any named function and define its behavior externally.

The Framework Should Handle Data Types

Our evaluator should be able to detect the data type of the values in an expression. For this to be done, we will use some standard language ticks. A string will be enclosed in simple quotes ('), the numbers will start with a digit and have an optional dot (.) for floating numbers, Booleans will be true and false, and date and times will need to be enclosed in sharps (#). Optionally, parser functions will be added to add casting capabilities.

Defining the Language

Extended Backus-Naur Form

The beauty of the BNF is that, being by essence a language to describe languages, it can be used to describe itself. This is like an English grammar book written in plain English. In order to define a language, we have to define all of its components and the links between them. For instance, an Addition can be represented with the sign + between two numbers. This rule can be written like this:

Collapse | Copy Code

addition : INTEGER '+' INTEGER ;
INTEGER : ('0'.. '9')+ ;

Those rules can be read as, "An integer is a character taken between 0 and 9 repeated at least one time," and "An addition is an integer followed by the character + and another integer." Those rules are obviously incomplete, but they give a good example of what the BNF notation is about. To be more precise, the notation used above is based on the Extended Backus-Naur form (EBNF), which simplifies it a lot while respecting the overall philosophy.

As you can see, addition is written in lower case as opposed to INTEGER, which is upper cased. In grammar, this means that the INTEGER rule is not dependent on any other rule. It is called a token and is detected by the lexer. In contrast, the lower-cased rules are analyzed by the parser and are non-terminal rules.

The Grammar

The first thing we have to care about is the operator precedence. In any logical expression, several parts must be evaluated in the correct sequence order. For instance, given the expression 2 + 3 * 5, we must evaluate the multiplicative expression first or it would result in a wrong value. The same applies to all operators, whether they be relational, additive, Boolean or any other. The table below enumerates all of the operators we will allow in the grammar, listed in their precedence order. This means that the higher it is in the table, the more priority it will have in the expression evaluation order.

Operator	Description
()	Grouping operator
!, not	Logical negation
*, /, %	Multiplicative operators
+, -	Additive operators
<, >, <=, >=	Relational operators
=, ==, !=, <>	Equality operators
&&, and	Logical and
\|\|, or	Logical or

To define this precedence, we have to use a specific recursive grammar pattern.

Collapse | Copy Code

logicalExpression
    :    booleanAndExpression ( OR booleanAndExpression )*
    ;

This rule defines the last element in the precedence list and by now all the succeeding rules will go higher in this table. The OR token describes the characters representing the logical or expression operator and will be described later in the grammar along with all other tokens. By default, if no OR operator is used, this rule will automatically try to analyze the next rule in the precedence list, which is the booleanAndExpression.

Collapse | Copy Code

booleanAndExpression
    :    equalityExpression ( AND equalityExpression )*
    ;

Here we define the booleanAndExpression as we did with the logicalExpression by optionally detecting the AND token. If not, the next rule will be analyzed.

Collapse | Copy Code

equalityExpression
    :    relationalExpression ( (EQUALS | NOTEQUALS) relationalExpression)*
    ;

Equality operators have both the same weight in the precedence list. Hence, if both are found successively, the one on the left side will be taken first.

Collapse | Copy Code

relationalExpression
    :    additiveExpression ( (LT | LTEQ | GT | GTEQ) additiveExpression)*
    ;

additiveExpression
    :    multiplicativeExpression ( (PLUS | MINUS) multiplicativeExpression )*
    ;

multiplicativeExpression
    :    unaryExpression (( MULT | DIV | MOD ) unaryExpression)*
    ;

unaryExpression
    :    NOT! primaryExpression
       ;

primaryExpression
    :    '(' logicalExpression ')'
    |    value
    ;

Here we define the most important rule in the precedence list, which is the primaryExpression. It is made of optional opening and closing parentheses containing another logicalExpression, thus allowing any expression inside. Note that we have still not defined the value rule. For the moment, suppose it represents all of the atomic real values that an expression can comprise. Now we can define all the tokens.

Collapse | Copy Code

OR    :     '||' | 'or';
AND   :     '&&' | 'and';
EQUALS
      :    '=' | '==';
NOTEQUALS
      :    '!=' | '<>';
LT    :    '<';
LTEQ  :    '<=';
GT    :    '>';
GTEQ  :    '>=';
PLUS  :    '+';
MINUS :    '-';
MULT  :    '*';
DIV   :    '/';
MOD   :    '%';
NOT   :    '!' | 'not';

Here we have defined all of the tokens needed by our grammar. You can notice that some tokens have several definitions such as OR, AND or NOT. I decided to let the user have the ability to use, for instance, both '||' and 'or' to define a Boolean or expression. This will give the user more flexibility. Now we need to define all the possible typed values:

Collapse | Copy Code

value    :    INTEGER
    |    FLOAT
    |    STRING
    |     DATETIME
    |    BOOLEAN
    ;

Later we define that a value can also be the evaluation of a function or a parameter.

Collapse | Copy Code

INTEGER
    :    '-'? ('0'..'9')+
    ;
FLOAT
    :    '-'? ('0'..'9')+ '.' ('0'..'9')+
    ;

STRING
     :    '\'' (~ '\'' )* '\''
     ;

Here we define the STRING token as a set of any characters instead of the simple quote between two simple quotes. In an ANTLR grammar, the simple quote must be escaped with \'.

Collapse | Copy Code

DATETIME
     :    '#' (~ '#' )* '#'
     ;

As for STRING, we accept any character between two sharps.

Collapse | Copy Code

BOOLEAN
    :    'true'
    |    'false'
    ;

ANTLR

Detecting the End of the Stream

Along with all those definitions, ANTLR needs some more information to generate a correct lexer/parser couple, like the targeted language and the name of the grammar.

Collapse | Copy Code

grammar ECalc;
options
{
    language=CSharp;
}

We also need to add another rule detecting the end of the stream.

Collapse | Copy Code

expression
    :     logicalExpression EOF
    ;

It will tell ANTLR that any terminal expression is made of an elementary logicalExpression.

Generating the Code

Now that we have a relatively complete grammar, we are able to generate the lexer and the parser. This can be done using the graphical tool AntlrWorks, available on the ANTLR website. The generated code is composed of two classes: ECalcParser and ECalcLexer.

Here is some code to test the behavior of our grammar.

Collapse | Copy Code

[Test]
public void ParserShouldHandleSimpleExpressions()
{
    ECalcLexer lexer = new ECalcLexer(new ANTLRStringStream("3*(5+2)"));
    ECalcParser parser = new ECalcParser(new CommonTokenStream(lexer));

   parser.expression();
}

Here we test a valid expression. It is done by instantiating a lexer and a parser. Then we call the expression() method of the parser instance. This method corresponds to the analysis of an expression rule defined in the grammar. We could also have asked the parser to identify, for instance, a multiplicativeExpression instead.

Collapse | Copy Code

[Test]
public void ParserShouldHandleBadExpressions()
{
    ECalcLexer lexer = new ECalcLexer(new ANTLRStringStream("3*(5+2"));
    ECalcParser parser = new ECalcParser(new CommonTokenStream(lexer));

    try
    {
        parser.expression();
        Assert.Fail();
    }
    catch (Exception e)
    {
        Console.Error.WriteLine("Parser exception: " + e.Message);
    }
}

Here we are trying to analyze a badly formatted expression. As you can see, a right parenthesis is lacking. The result of the method is this one below.

Collapse | Copy Code

Error: line 0:-1 mismatched input '<eof />' expecting ')'

Creating the AST

When evaluating an expression, the parser generated by ANTLR is able to go through all the rules like this:

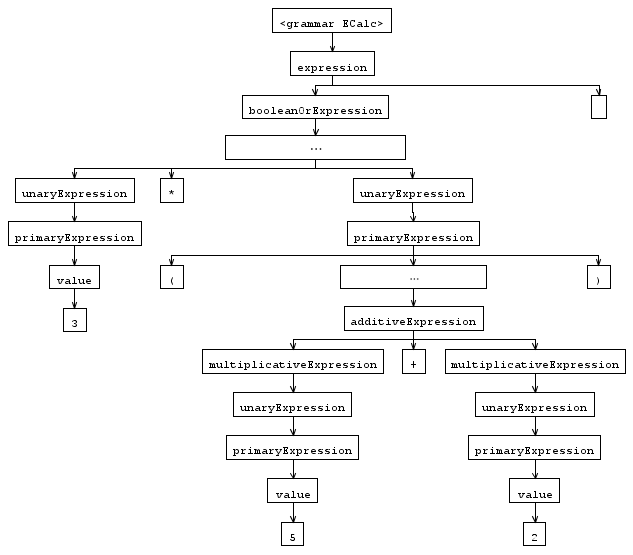
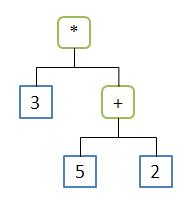
Here we evaluated the expression 3 * (5 + 2). This graph was generated by AntlrWorks. We do not need this level of detail to handle expressions. The precedence hierarchy for instance is only useful at the parser level. Instead we need a tree defining this precedence with the operators as the root like the schema below.

ANTLR can embed in the grammar the instructions driving the creation of this AST (Abstract Syntax Tree). As programmers, we should be able to handle the finalized ordered tree representing the expression. Tree structures are very useful data structures in object programming. Moreover, we will be able to create specific Visitors (see Visitor Pattern) to handle our expressions with different logic: display, evaluations, simplification, etc. Besides this, we can also remove elements that we do not want to see in our AST. This is the case of all "punctuations," namely the commas, parentheses, etc. Look at the complete grammar in the source code to see the constructs of those elements. Once the grammar is modified to handle the tree structure, here is the code to display this tree.

Collapse | Copy Code

[Test]
public void ParserShouldHandleTree()
{
    ECalcLexer lexer = new ECalcLexer(new ANTLRStringStream("3*(5+2)"));
    ECalcParser parser = new ECalcParser(new CommonTokenStream(lexer));

    CommonTree tree = (CommonTree)parser.expression().Tree;
    Console.WriteLine(tree.ToStringTree());
}

And the result:

Collapse | Copy Code

(* 3 (+ 5 2))

Transforming the AST

At this point, we are able to go through any node of the AST representing our expression. We could use this structure to start our evaluation, but as stated earlier, this would be a flow for the evolution of the Framework. Instead, we will create a tree representation using our own business classes, with a more meaningful model.

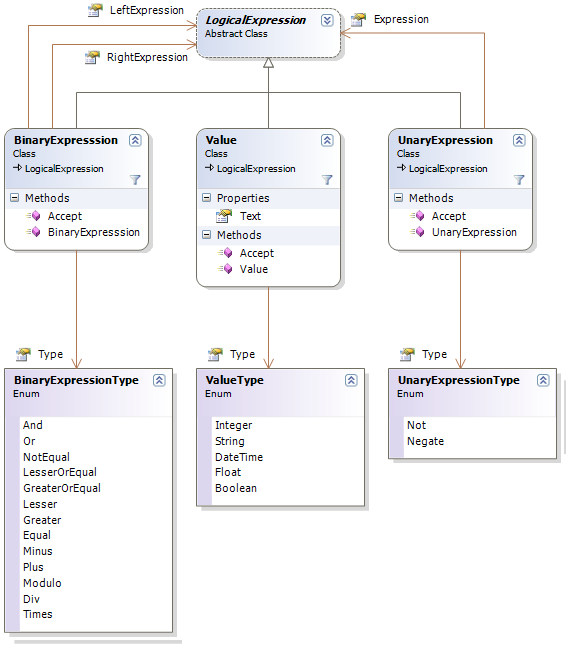
This model factors all binary expressions into a single class. The difference is made using a specific enumeration. The creation of this model is done using a dedicated static method in the class LogicalExpression.

Collapse | Copy Code

public static LogicalExpression Create(CommonTree ast)
{
    if (ast == null)
        throw new ArgumentNullException("tree");

    switch (ast.Type)
    {
        case ECalcParser.INTEGER:
            return new Value(ast.Text, ValueType.Integer);

        /* ... */

        case ECalcParser.NOT:
            return new UnaryExpression(UnaryExpressionType.Not,
                Create((CommonTree)ast.GetChild(0)));

        /* ... */

        case ECalcParser.MULT:
            return new BinaryExpresssion(BinaryExpressionType.Times,
                Create((CommonTree)ast.GetChild(0)),
                Create((CommonTree)ast.GetChild(1)));

        /* ... */

        case ECalcParser.LT:
            return new BinaryExpresssion(BinaryExpressionType.Lesser,
                Create((CommonTree)ast.GetChild(0)),
                Create((CommonTree)ast.GetChild(1)));

        /* ... */

        case ECalcParser.AND:
            return new BinaryExpresssion(BinaryExpressionType.And,
                Create((CommonTree)ast.GetChild(0)),
                Create((CommonTree)ast.GetChild(1)));

        default:
            return null;
    }
}

Anything in this model inherits from LogicalExpression as any piece of a mathematical expression can be comprised in a binary expression or a unary expression. For instance in 3 * (5 + 2) the Times operator -- a binary expression -- will have the Value 3 as its left expression. The Plus operator will have the values 5 and 2 respectively for its left and right expressions. Later, we will be able to put functions and parameters that will be evaluated dynamically. We will also have to inherit from LogicalExpression to take right into the model. In this method, we will add a special case to handle the declaration and instantiate the corresponding object.

Evaluation

Visitor Pattern

On top of the model, the visitor pattern is implemented. It means that any logic can be externalized from the object model itself. One of these logics is for the dynamic evaluation of the model.

Collapse | Copy Code

public abstract class LogicalExpressionVisitor
{
    public abstract void Visit(LogicalExpression expression);
    public abstract void Visit(BinaryExpresssion expression);
    public abstract void Visit(UnaryExpression expression);
    public abstract void Visit(Value expression);
}

Evaluating the values is simple. It consists of switch casing and parsing the text using the correct type.

Collapse | Copy Code

public override void Visit(Value expression)
{
    switch (expression.Type)
    {
        case ValueType.Boolean:
            result = bool.Parse(expression.Text);
            break;

        case ValueType.DateTime:
            result = DateTime.Parse(expression.Text);
            break;

        case ValueType.Float:
            result = decimal.Parse(expression.Text, numberFormatInfo);
            break;

        case ValueType.Integer:
            result = int.Parse(expression.Text);
            break;

        case ValueType.String:
            result = expression.Text;
            break;
    }
}

As you can see, the result of the evaluation is stored in a member named result. The class EvaluationVisitor also exposes a getter property to read this value. Notice that for floating point number parsing, we need to define a NumberFormatInfo instance. Most programmers wouldn't have cared about it, but on a system with no English culture, floating point numbers might be written with a coma (,) instead of the dot (.). My own system is set up in French. Thus, in the constructor of EvaluationVisitor we override this by forcing to use the dot. This could be enhanced to let the user choose which culture he wants to apply.

Collapse | Copy Code

public override void Visit(UnaryExpression expression)
{
    // Recursively evaluates the underlying expression
    expression.Expression.Accept(this);

    switch (expression.Type)
    {
        case UnaryExpressionType.Not:
            result = !Convert.ToBoolean(result);
            break;
    }
}

To evaluate UnaryExpression, the underlying one needs to be evaluated first. We can call the same visitor on this expression for this. The result can then be retrieved in result and negated if it is really a Boolean value.

Collapse | Copy Code

public override void Visit(BinaryExpresssion expression)
{
    // Evaluates the left expression and saves the value
    expression.LeftExpression.Accept(this);
    object left = result;

    // Evaluates the right expression and saves the value
    expression.RightExpression.Accept(this);
    object right = result;

    switch (expression.Type)
    {
        case BinaryExpressionType.And:
            result = Convert.ToBoolean(left) && Convert.ToBoolean(right);
            break;

        /* ... */

        case BinaryExpressionType.Equal:
            // Use the type of the left operand to make the comparison
            result = Comparer.Default.Compare(left,
                Convert.ChangeType(right, left.GetType())) == 0;
            break;

        /* ... */

        case BinaryExpressionType.Plus:
            result = Convert.ToDecimal(left) + Convert.ToDecimal(right);
            break;

        case BinaryExpressionType.Times:
            result = Convert.ToDecimal(left) * Convert.ToDecimal(right);
            break;
    }
}

As for the UnaryExpression evaluation, we need to evaluate both the left and right expressions for BinaryExpression. Then we can switch on its type to execute the corresponding logic. The only thing to care about here is the type matching. For instance, we could write an equality comparison between two different types as we work with objects internally. Hence, we must convert items to make their types match. A good solution is to decide to use the type of the left member and use its default comparer to compare with the right member. Concerning the numerical operations, all of the values are converted to Decimal in order not to lose any information during conversion to integral types.

Using the Visitor

Here is the code needed to evaluate any expression tree made of our domain classes.

Collapse | Copy Code

BinaryExpresssion expression =
     LogicalExpression.Create(Parse("3 * (5 + 2)")) as BinaryExpresssion;

EvaluationVisitor visitor = new EvaluationVisitor();
Expression.Accept(visitor);
Assert.AreEqual(21, visitor.Result);

The "visit" of any instance is recursive. Hence, we can give the root of the expression tree to the visitor and once the process is done, we can read the final result. In this code, we first create the tree representing the expression using the Parse() method. It returns an instance of LogicalExpression and uses ECalcParser and ECalcLexer used earlier. In this case, it returns a BinaryExpression value standing for the Times operator (Fig. 1). The traversal of this tree is made from the leaves to the root. The leaves are the most important expressions in the precedence order, as the grammar was declared for the parsing operations to use this information.

Collapse | Copy Code

- Visit BinaryExpression (* 3 (+ 5 2))
            { Type:Times; Left:3; Right:(+ 5 2) } -> 21
    - Visit Value 3 { Type:Integer; Text:3 } -> 3
    - Visit BinaryExpression (+ 5 2) { Type:Plus; Left:5; Right:2 } -> 7
        - Visit Value 5 { Type:Integer; Text:5 } -> 5
        - Visit Value 2 { Type:Integer; Text:2 } -> 2

Here is the table of calls while evaluating the tree.

Creating the Framework

The Expression Class

To simplify all of this work, we need to provide the user with a single class representing a textual expression and returning the value of its evaluation.

Collapse | Copy Code

public class Expression
{
    protected string expression;

    public Expression(string expression)
    {
        if (expression == null || expression == String.Empty)
            throw new
                ArgumentException("Expression can't be empty", "expression");

        this.expression = expression;
    }

    public CommonTree Parse(string expression)
    {
        ECalcLexer lexer = new ECalcLexer(new ANTLRStringStream(expression));
        ECalcParser parser = new ECalcParser(new CommonTokenStream(lexer));

        return (CommonTree)parser.expression().Tree;
    }

    public object Evaluate()
    {
        EvaluationVisitor visitor = new EvaluationVisitor();
        LogicalExpression.Create(Parse(expression)).Accept(visitor);
        return visitor.Result;
     }
}

Now we can use this simple Expression class.

Collapse | Copy Code

public void ExpressionShouldEvaluate()
{
    string[] expressions = new string[]
    {
        "2 + 3 + 5",
        "2 * 3 + 5",
        "2 * (3 + 5)",
        "2 * (2*(2*(2+1)))",
        "10 % 3",
        "true or false",
        "false || not (false and true)",
        "3 > 2 and 1 <= (3-2)",
        "3 % 2 != 10 % 3",
    };

    foreach(string expression in expressions)
        Console.WriteLine("{0} = {1}",
            expression,
            new Expression(expression).Evaluate());
}

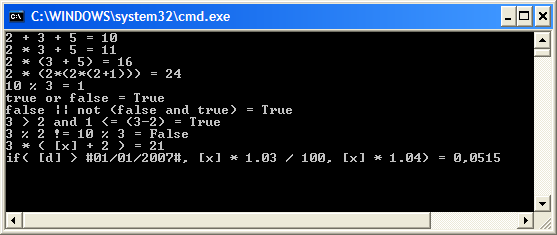
2 + 3 + 5 = 10
2 * 3 + 5 = 11
2 * (3 + 5) = 16
2 * (2*(2*(2+1))) = 24
10 % 3 = 1
true or false = True
false || not (false and true) = True
3 > 2 and 1 <= (3-2) = True
3 % 2 != 10 % 3 = False

Here are some examples of expressions we can evaluate using our new class.

Enhancing the Grammar

Mathematical Functions

Our expression evaluator is now fully functional, but we need some more capabilities to make it really useful. First, we need more enhanced mathematical tools than the simple arithmetic operations, i.e. trigonometry, rounding, etc. This will be done by adding a new concept to our grammar: the functions. This will be a concrete exercise to see if our Framework is flexible enough. A function is made of an identifier and a list of parameters between parentheses. Those parameters can be anything, even logical expressions.

Collapse | Copy Code

function
    :    IDENT '(' ( logicalExpression (',' logicalExpression)* )? ')'
    ;

Here we define the function rule as an identifier -- i.e. the name of the function -- and an optional set of comma-separated arguments. Those arguments can be any other sub expression.

Collapse | Copy Code

IDENT
    :    ('a'..'z' | 'A'..'Z' | '_') ('a'..'z' | 'A'..'Z' | '_' | '0'..'9')*
    ;

An identifier is the name of the function. It can be of any character case and must start with a letter.

Collapse | Copy Code

value    :    INTEGER
    |    FLOAT
    |    STRING
    |     DATETIME
    |    BOOLEAN
  |    function
    ;

We also need to update the value rule to allow a function to be part of the expression tree at any place a value can be. Those rules can be added directly to the grammar file. Then we generate the code for the lexer and parser using AntlrWorks and we overwrite our current classes. As it is a new concept, this rule should not conflict with our current implementation and actually it doesn't. Then we need to add this new concept to our domain model and update the LogicalExpression.Create() method to handle its creation.

The Function class contains an Identifier property representing the name of the function, as well as a list of LogicalExpression instances for its parameters.

Collapse | Copy Code

case ECalcLexer.IDENT:
    LogicalExpression[] expressions = new LogicalExpression[ast.ChildCount];

    for(int i=0; i < ast.ChildCount; i++)
        expressions[i] = LogicalExpression.Create((CommonTree)ast.GetChild(i));

    return new Function(ast.Text, expressions);

Now we can handle the visit of this class. What has to be done is the declaration of all mathematical functions we want to handle. The behavior must be switched using the identifier. Thus, the syntax of function-calling is not handled in the grammar. This can imply some flows as, for instance, the number of allowed parameters for each function will not be detected by the parser, but while dynamically evaluating the Function instance. However, it also allows our code to handle any function without needing any change in the grammar. Next, we'll see how it can be powerful.

Collapse | Copy Code

case "Abs":

    if (function.Expressions.Length != 1)
        throw new ArgumentException("Abs() takes exactly 1 argument");

    result = Math.Abs(Convert.ToDecimal(
        Evaluate(function.Expressions[0]))
        );

    break;

As you can see, it is very simple to implement any logic for a function. The only thing to do is test the number of given parameters. Hence, we can implement all of the methods found in the System.Math class.

Collapse | Copy Code

Assert.AreEqual(1, new Expression("Abs(-1)").Evaluate());
Assert.AreEqual(0, new Expression("Acos(1)").Evaluate());
Assert.AreEqual(0, new Expression("Asin(0)").Evaluate());
Assert.AreEqual(0, new Expression("Atan(0)").Evaluate());
Assert.AreEqual(2, new Expression("Ceiling(1.5)").Evaluate());
Assert.AreEqual(1, new Expression("Cos(0)").Evaluate());
Assert.AreEqual(1, new Expression("Exp(0)").Evaluate());
Assert.AreEqual(1, new Expression("Floor(1.5)").Evaluate());
Assert.AreEqual(-1, new Expression("IEEERemainder(3,2)").Evaluate());
Assert.AreEqual(0, new Expression("Log(1,10)").Evaluate());
Assert.AreEqual(0, new Expression("Log10(1)").Evaluate());
Assert.AreEqual(9, new Expression("Pow(3,2)").Evaluate());
Assert.AreEqual(3.22, new Expression("Round(3.222,2)").Evaluate());
Assert.AreEqual(-1, new Expression("Sign(-10)").Evaluate());
Assert.AreEqual(0, new Expression("Sin(0)").Evaluate());
Assert.AreEqual(2, new Expression("Sqrt(4)").Evaluate());
Assert.AreEqual(0, new Expression("Tan(0)").Evaluate());

Here you can see all of the implemented mathematical functions and their various tests.

Scripting Functions

Mathematical functions are useful, but couldn't we implement more clever ones? One function I like in Microsoft Excel is the IF THEN ELSE construct. It allows us to define a cell using conditional statements. In our Framework, we can add it very easily using a specific function. Here is a possible syntax: if(condition, value if true, value if false). To implement it, we just need to add the management of the if identifier in the visit of the Function class.

Collapse | Copy Code

case "if":

    if (function.Expressions.Length != 3)
        throw new ArgumentException("if() takes exactly 3 arguments");

    bool cond = Convert.ToBoolean(Evaluate(function.Expressions[0]));
    object then = Evaluate(function.Expressions[1]);
    object els = Evaluate(function.Expressions[2]);

    result = cond ? then : els;
    break;

If you have a little bit of imagination, you may imagine how to create your own scripting language with this technique. For instance, I use this Framework in several applications as a rule engine to externalize some of the logic and workflows.

Custom Functions

At that point, ideas should start emerging on how to use his Framework. However, you might be limited by the variety of the available functions. You know how to add new methods, but it implies modifying the EvaluationVisitor class and this is not a viable technique. This leads us to implement a method of adding new functions dynamically. Implementing custom functions could be done using different techniques. For simplicity, I decided to use delegates. When evaluating functions, we will first call a specific delegate we can register to. A class, FunctionArgs, would handle the information of the called function and we would return the result of our custom evaluation using a callback parameter.

Collapse | Copy Code

public class FunctionArgs : EventArgs
{
    public FunctionArgs()
    {
    }

    private object result;

    public object Result
    {
        get { return result; }
        set { result = value; }
    }

    private object[] parameters = new object[0];

    public object[] Parameters
    {
        get { return parameters; }
        set { parameters = value; }
    }
}

We also create a specific handler named EvaluateFunctionHandler. In the function's evaluation code, we then have to call any method registered to the event and get the callback result. This invocation is done before the evaluation of any internal function, which will allow the user to override its implementation. If no result is returned, we then call the internal functions.

Collapse | Copy Code

public override void Visit(Function function)
{
    // Evaluates all parameters
    object[] parameters = new object[function.Expressions.Length];
    for (int i = 0; i < parameters.Length; i++)
        parameters[i] = Evaluate(function.Expressions[i]);

    FunctionArgs args = new FunctionArgs();
    args.Parameters = parameters;

    // Calls external implementation
    OnEvaluateFunction(function.Identifier, args);

    // If an external implementation was found get the result back
    if (args.Result != null)
    {
        result = args.Result;
        return;
    }

    switch (function.Identifier)
    {
        /* ... */
    }
}

This event is defined in EvaluationVisitor. To make it accessible to the user, we also need to handle it in the Expression class. At this point, the user can add any new function.

Collapse | Copy Code

Expression e = new Expression("SecretOperation(3, 6)");
e.EvaluateFunction += delegate(string name, FunctionArgs args)
    {
        if (name == "SecretOperation")
            args.Result = (int)args.Parameters[0] + (int)args.Parameters[1];
    };

Assert.AreEqual(9, e.Evaluate());

Here the anonymous method syntax of C# 2.0 is used, but in .NET 1.1 the standard delegates can be used. A concrete use of this technique would be to return business-aware methods depending on the domain of the application using the Framework. For financial applications, this could return stock rates or define taxes using ranges with a between function like the if method. Moreover, an extension to this behavior could be to create a specific abstract class that the user could inherit to define a specific function and would add this type to the visitor. This would be the first step to a real plug-in system.

Parameters

Most operations need external input. We could create new expressions by concatenating those external values and the actual expression, but this is just plumbing and not programming. Thus, we need to add parameter management. The grammar has to be modified by adding this concept. We define a parameter as an identifier between squares. The identifier can also start with an integer to be able to define expressions like this: Sqrt(Pow([0], 2) + Pow([1], 2)). Here are the modifications we have to apply to our grammar.

Collapse | Copy Code

parameter
    :    '[' (IDENT|INTEGER) ']';

value    :    INTEGER
    |    FLOAT
    |    STRING
    |     DATETIME
    |    BOOLEAN
    |    function
    |    parameter
    ;

To handle the evaluation of those parameters, the same technique as for the custom functions will be used. Another delegate is added to let the user define a method that is able to evaluate parameters.

Collapse | Copy Code

public override void Visit(Parameter parameter)
{
    if (parameters.Contains(parameter.Name))
    {
        // The parameter is defined in the hashtable
        if (parameters[parameter.Name] is Expression)
        {
            // The parameter is itself another Expression
            Expression expression = (Expression)parameters[parameter.Name];
            expression.Parameters = parameters;
            expression.EvaluateFunction += EvaluateFunction;
            expression.EvaluateParameter += EvaluateParameter;

            result = ((Expression)parameters[parameter.Name]).Evaluate();
        }
        else
            result = parameters[parameter.Name];
    }
    else
    {
        // The parameter should be defined in a call back method
        ParameterArgs args = new ParameterArgs();

        // Calls external implementation
        OnEvaluateParameter(parameter.Name, args);

        if (args.Result == null)
            throw new ArgumentException("Parameter was not defined",
                 parameter.Name);

        result = args.Result;
    }
}

As you can see, there are two possibilities to define parameters:

With a dedicated Hashtable or
Using a callback method as we did with the functions

Collapse | Copy Code

public void ExpressionShouldEvaluateParameters()
{
    Expression e = new Expression
    ("Round(Pow([Pi], 2) + Pow([Pi2], 2) + [X], 2)");

    e.Parameters["Pi2"] = new Expression("[Pi] * [Pi]");
    e.Parameters["X"] = 10;

    e.EvaluateParameter += delegate(string name, ParameterArgs args)
        {
            if (name == "Pi")
                args.Result = 3.14;
        };

    Assert.AreEqual(117.07, e.Evaluate());
}

In this not-so-simple example, you can see the three techniques of passing parameters to an expression.

Possible Evolutions

The first one is for performance enhancement. Currently, I'm using an original version of this Framework in which I implemented a cache. Thus, I can compile an expression once and run it as many times as I want without needing to parse the expression each time. Then I can vary all of the parameters without worrying about the time to process the string representation.

The function list can also be enhanced. Currently, there is no method to manipulate DateTime types. There are also not many more for strings.

Maybe I'll refactor the code a little bit to explode BinaryExpression and the other classes into separate concepts like OrExpression, NotExpression, etc. It will not change the behavior, but it will allow a more flexible evolution for new expressions. It will also make the visitor less "switchcase-ish" by using more polymorphism.

Conclusion

This Framework is a good demonstration of how to make domain-specific languages and create interpreters for them. If you didn't know about ANTLR, I hope that you are now confident about its capabilities. A note on performance: If you try to compare this technique with the most widely used technique of dynamic compilation using CodeDom, you will see that the technique discussed in this article is far more powerful, as there is no memory leakage and it is also much faster.

Resources

The ANTLR website

History

Bug fix and new feature (14 November 2007)
- Corrected escape characters management with spaces (zuken21)
- Added error management, the evaluation throws an EvaluationException with a description message
Escape characters improvements (1 November 2007)
- Added escape characters management
- Added Unicode escape characters management
Bug fix (18 July 2007)
- Changed grammar to add the power operator ^ as requested by Aldy (dummy1807)
- Corrected bugs in string values submitted by Brian Drevicky
Bug fix (31 May 2007)
- Changed grammar since the NEGATE unary expression was not added in the AST causing a Null Reference Exception (thanks to beep)
- Moved the test classes into a separate project
Original version posted (22 May 2007)

State of the Art Expression Evaluation

Introduction

Approach

Defining the Language

Lexer and Parser

Execution Engine

Stories

Principle

The User Should Be Able to Evaluate the String Representation of a Logical Expression

The User Should Be Able to Define Parameters

The User Should Be Able to Use Predefined Mathematical Functions

The User Should Be Able to Use His Own Functions

The Framework Should Handle Data Types

Defining the Language

Extended Backus-Naur Form

The Grammar

ANTLR

Detecting the End of the Stream

Generating the Code

Creating the AST

Transforming the AST

Evaluation

Visitor Pattern

Using the Visitor

Creating the Framework

The Expression Class

Enhancing the Grammar

Mathematical Functions

Scripting Functions

Custom Functions

Parameters

Possible Evolutions

Conclusion

Resources

History

License

About the Author